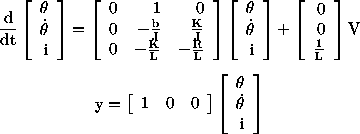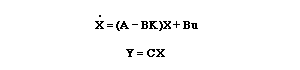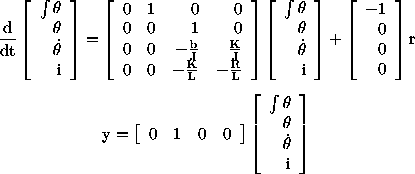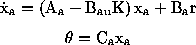CTM Ejemplo: Diseño en espacio de estados para un control de posición de un motor de corriente continua

Ejemplo Tutorial: Realimentación de Estados para un Control de Posición de un Motor de Corriente Continua

(Traducido de uno de los Ejemplos Tutoriales de Control de la Carnegie Mellon University.)

Diseño del controlador por realimentación de estados
Respuesta a perturbaciones
Agregado de acción integral

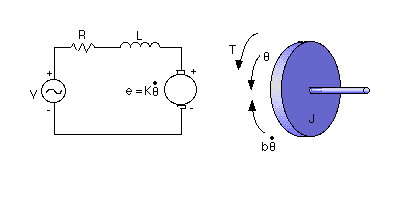
Las ecuaciones dinámicas en espacio de estados del motor son las siguientes:

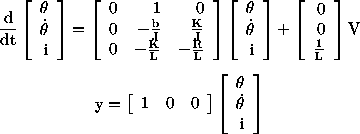
Con una referencia de 1 radian agregada al sistema, los criterios de diseño son:

Tiempo de establecimiento menor que 0.04 segundos
Sobrevalor menor que 16%
Cero error estático de posición a una entrada escalón
Cero error estático de posición a una perturbación escalón

Editemos un nuevo archivo-m con los siguientes comandos:

J=3.2284E-6;              
b=3.5077E-6;              
K=0.0274;
R=4;
L=2.75E-6;

A=[0 1 0
   0 -b/J K/J
   0 -K/L -R/L];
B=[0 ; 0 ; 1/L];
C=[1 0 0];
D=[0];

Diseño del controlador por realimentación de estados

Como todas las variables de estado en nuestro problema son muy fáciles de medir (un amperímetro para la corriente, un taquímetro para la velocidad, y un potenciómetro para la posición), podemos diseñar un controlador por realimentación de estados completo sin preocuparnos por estimar ningún estado con observador. El esquema para la realimentación de estados es:

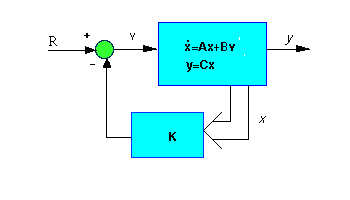
Recordemos que el polinomio característico para este sistema a lazo cerrado es el determinante de (sI-(A-BKc)) donde s es la variable de Laplace. Como las matrices A y B*Kc son las dos 3x3, debe haber 3 polos para el sistema. Mediante realimentación de estados podemos mover estos polos a voluntad. Vamos a tratar primero de colocarlos en -100 + 100i y -100-100i (que corresponden a un sistema de segundo orden con un amortiguamiento zeta = 0.5, que da un sobrevalor de 16%, y un sigma = 100 que da un tiempo de establecimiento de 0.04 segundos). Una vez que elegimos los polos que queremos, Matlab nos va a hallar la matriz Kc. Simplemente agregamos lo siguiente al final del archivo-m

p1=-100+100i;
p2=-100-100i;
p3=-200;
Kc=place(A,B,[p1,p2,p3]);

Volvamos al esquema de arriba. Vemos que una vez incorporada la matriz K al sistema, las ecuaciones de estado pasan a ser:

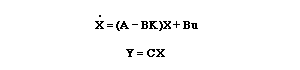
Podemos ver la respuesta del lazo cerrado simplemente agregando la siguiente línea al final del archivo-m:

t=0:0.001:.05;
step(A-B*Kc,B,C,D,1,t)

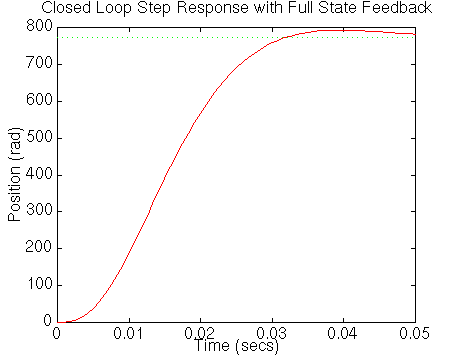
Corriendo el archivo-m en la ventana de comandos de Matlab, deberíamos obtener la siguiente figura:

Respuesta a Perturbaciones

Para obtener la respuesta a una perturbación tenemos que incluir una entrada adecuada al sistema. Físicamente, una perturbación es un torque que actúa sobre la inercia del motor. Un torque actúa como un término aditivo en la segunda ecuación de estados (que queda dividido por J, como los demás términos en esta ecuación). Podemos simular esta perturbación simplemente modificando la matriz de entrada de lazo cerrado, B, para que tenga 1/J en la segunda fila. Agreguemos la siguiente línea a nuestro archivo-m y corrámoslo nuevamente.

step(A-B*Kc,[0;1/J;0],C,D,1,t)

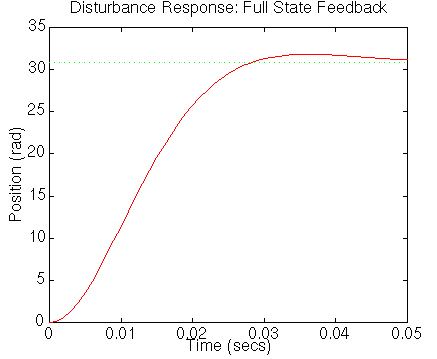
Esta no es una respuesta con error estático cero, así que vamos a tener que compensar.

Agregado de Acción Integral

Sabemos que si ponemos un integrador extra en serie con la planta va a eliminar el error estático a una entrada. Si el integrador viene antes del punto de inyección de la perturbación, cancelará la perturbación en régimen permanente. Esto cambia la estructura de control, que queda ahora de la forma siguiente:

Podemos modelar el integrador aumentando nuestras ecuaciones de estado con un estado extra que es la salida del integrador. Esto agrega una ecuación extra que establece que la derivada de la integral de theta es theta. Colocaremos esta ecuación encima de nuestras matrices. La entrada, r, ahora entra al sistema antes del integrador, asi que aparece en la recientemente agregada ecuación de arriba. La salida del sistema queda igual.

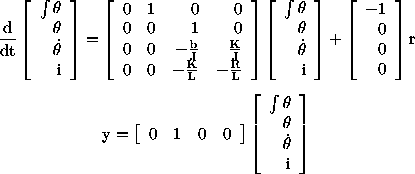
Estas ecuaciones representan la dinámica del sistema antes de cerrar el lazo. Denotaremos las matrices en esta ecuación como A_a, B_a, C_a, y D_a. Denotaremos el vector de estados del sistema aumentado como x_a. Notar que la referencia, r, no afecta los estados (excepto por el estado del integrador) o la salida de la planta - lo que es obvio pues no hay ninguna conexión entre la referencia y la entrada de la planta, u, sin implementar la matriz de realimentación de estados Kc.

Para hallar las ecuaciones de lazo cerrado tenemos que examinar cómo afecta la entrada, u, a la planta. En este caso es exactamente de la misma forma que en las ecuaciones aumentadas. Por lo tanto, existe un vector, llamémoslo B_au, que reemplaza B_a cuando tomamos a u como la entrada. Éste no es más que nuestro viejo vector B con un cero extra agregado en la primer fila. Como u=Kc*x_a es la entrada a la planta para el lazo cerrado, pero r es la entrada al sistema a lazo cerrado, las ecuaciones de lazo cerrado dependen de ambas B_au and B_a. Las ecuaciones de lazo cerrado entonces quedan:

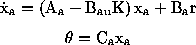
Ahora, la integral de la salida se realimenta, y va a ser usada por el controlador para eliminar el error estático originado por la perturbación. Ahora podemos rediseñar nuestro controlador. Como tenemos que ubicar un polo a lazo cerrado por cada polo en la planta, vamos a ubicar otro polo en -300, que va a ser más rápido que el resto de los polos. Como la matriz del sistema a lazo cerrado depende de B_au, vamos a usar B_au en el comando place en vez de B_a. Agregamos los siguiente a nuestro archivo-m.

Aa=[0 1 0 0
    0 0 1 0 
    0 0 -b/J K/J
    0 0 -K/L -R/L];
Ba=[ -1 ; 0 ; 0 ; 0];
Bau=[0 ; 0 ; 0 ; 1/L ];
Ca=[0 1 0 0];
Da=[0]; 

p4=-300;
Kc=place(Aa,Bau,[p1,p2,p3,p4]);

t=0:0.001:.05;
step(Aa-Bau*Kc,Ba,Ca,Da,1,t)

Corriendo el archivo-m (o sólo estas nuevas líneas) obtenemos la siguiente salida.

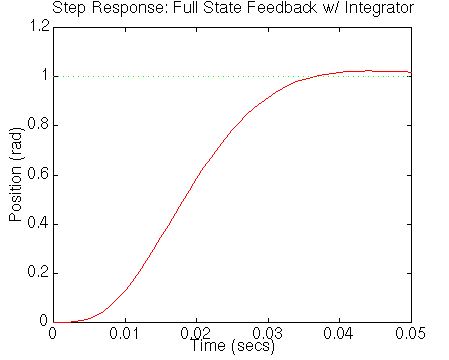
Para ver la respuesta a la perturbación, usamos una matriz B similar a la que usamos antes cuando simulamos la respuesta a la perturbación.

step(Aa-Bau*Kc,[0 ; 0 ; 1/J ; 0] ,Ca,Da,1,t)

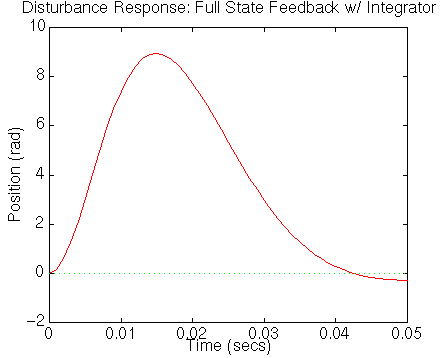
Vemos que todas los criterios de diseño han sido satisfechos por este controlador.