CTM Ejemplo: Diseño en espacio de estados para un control de posición de un motor de corriente continua

Ejemplo Tutorial: Diseño en espacio de estados para un péndulo invertido

(Traducido y adaptado de uno de los Ejemplos Tutoriales de Control de la Carnegie Mellon University.) pendulo

Polos a lazo abierto
Diseño óptimo LQR
Agregado de la entrada de referencia
Diseño del Observador

Las ecuaciones en espacio de estados del sistema son:

Los criterios de diseño con para una referencia escalón de 0.2m en el carro son los siguientes:

Tiempo de establecimiento para x y theta de menos de 5 segundos.
Tiempo de subida para x de menos de 1 segundo.
Sobrevalor en theta menor que 20 grados (0.35 radianes).
Error en régimen permanente dentro del 2%.

Este sistema tiene una entrada y dos salidas. Usando los métodos de EE es relativamente simple diseñar un controlador para conseguir seguimiento en ambas salidas, ángulo y posición del carro.

El problema puede resolverse con realimentación de estados. El esquema del lazo de control es el siguiente:

En la página Inverted Péndulo Animation se puede correr una animación on-line del péndulo en este ejemplo.

Polos a lazo abierto

En este problema R representa la entrada escalón al carro. Los 4 estados representan la posición y velocidad del carro y el ángulo y velocidad angular del péndulo. La salida y contiene la posición del carro y el ángulo del péndulo. Deseamos diseñar un controlador tal que cuando se le dé una entrada escalón al sistema, el péndulo se desplace (no hay otra posibilidad), pero que eventualmente vuelva a la posición de equilibrio (la vertical), y que el carro se mueva a la nueva posición de referencia. Intuitivamente (o por experiencia práctica) sabemos que el sistema es inestable a lazo abierto.

El primer paso en el diseño de este tipo de controlador es determinar los polos a lazo abierto. Entrar las siguientes líneas de código en un archivo-m:

     M = 0.5;
     m = 0.2;
     b = 0.1;
     i = 0.006;
     g = 9.8;
     l = 0.3;

     p = i*(M+m)+M*m*l^2; %denominator
     A = [0      1             0        0;
               0 -(i+m*l^2)*b/p (m^2*g*l^2)/p  0;
               0      0             0        1;
               0 -(m*l*b)/p    m*g*l*(M+m)/p 0];
     B = [0; (i+m*l^2)/p; 0; m*l/p];
     C = [1 0 0 0;
          0 0 1 0];
     D = [0;0];

     p = eig(A)

La ventana de comando de Matlab debería dar el siguiente resultado:

   p =
       0 -0.1428 5.5651 -5.6041

Como se ve, hay un polo inestable en 5.5651. Esto confirma la intuición de que el sistema es inestable a lazo abierto.

Diseño óptimo LQR

Aunque no vimos control óptimo todavía, la función de Matlab lqr que calcula la ganancia óptima LQR (Linear Quadratic Regulator --- regulador lineal óptimo cuadrático) es tan simple de usar como la place.

Entonces, el siguiente paso es asumir que disponemos del estado completo para la realimentación, y calcular la ganancia K que determina la ley de control u = -Kx. Esta ganancia puede calcularse de varias formas. Si uno ya sabe dónde quiere colocar los polos a lazo cerrado puede usar la función place o acker.

Otra opción es usar la función lqr; ésta da un controlador óptimo (bajo ciertas condiciones que veremos en detalle más adelante). La función lqr permite elegir dos parámetros, R y Q, que balancean la importancia relativa de la entrada y el estado en el costo que se pretende optimizar. El caso más simple es asumir R=1, y Q=C'*C. Notar que usamos las dos salidas (el ángulo del péndulo y la posición del carro). El método lqr permite manejar las dos salidas y en este caso es bastante fácilde hacerlo. El controlador puede ajustarse cambiando los elementos distintos de cero en la matriz Q hasta obtener una respuesta satisfactoria.

Para encontrar la estructura de Q entrar la siguiente línea en la ventana comando de Matlab:

   C'*C

Debería obtenerse:

El elemento (1,1) será usado para pesar la posición del carro, y el elemento (3,3) para pesar el ángulo del péndulo. Dejamos el peso en el control R=1. Ahora que sabemos qué forma tiene Q, podemos experimentar hasta encontrar la matriz K que nos da un buen controlador. Hacemos un programita para que los cambios en Q se vean automáticamente en la respuesta del controlador obtenido para cada iteración hasta encontrar la Q - y K - que satisfacen los requerimientos de diseño. Agregar las siguientes líneas en el archivo-m:

     x=1;
     y=1;
     Q=[x 0 0 0; 0 0 0 0; 0 0 y 0; 0 0 0 0];
     R = 1;
     K = lqr(A,B,Q,R)
     Ac = [(A-B*K)];
     Bc = [B];
     Cc = [C];
     Dc = [D];
     T=0:0.01:5;
     U=0.2*ones(size(T));
     [Y,X]=lsim(Ac,Bc,Cc,Dc,U,T);
     plot(T,Y)
     legend('Carro','Péndulo')

Debería obtenerse el siguiente valor de K y correspondiente respuesta:

   K =
       -1.0000 -1.6567 18.6854 3.4594

La curva en verde representa el ángulo, en radianes, y la curva en azul la posición, en metros. Como se ve, la respuesta no es satisfactoria. El sobrevalor en el ángulo está bien, pero los tiempos de establecimiento necesitan ajuste. Puede verse también que el carro no está cerca de la posición deseada sino que se movió para el lado opuesto. Corregiremos este error en la sección siguiente; por ahora nos concentramos en los tiempos de subida y establecimiento.

Volviendo al archivo-m, cambiamos las variables x e y para ver si se puede obtener una respuesta mejor. Vemos que aumentando x reducimos los tiempos de establecimiento y subida, y bajamos el ángulo que se mueve el éndulo. Usando x=5000 e y=100, se obtiene el siguiente valor de K y respuesta a lazo cerrado:

   K =
       -70.7107 -37.8345 105.5298 20.9238

Notamos que incrementando x e y aún más podríamos haber mejorado la respuesta más todavía. Elegimos estos valores porque satisfacen las especificaciones y mantienen x e y relativamente chicos. Cuando mayores sean x e y, mayor será el esfuerzo de control usado, y mayor el ancho de banda del sistema a lazo cerrado. El sistema tiene ahora un tiempo de establecimiento de 2 segundos.

Agregado de la entrada de referencia

Ahora eliminaremos el error estático. Usamos una matriz de precompensación Nbar en la forma mostrada en la figura:

Nbar puede encontrarse usando la función rscale (copiarla al directorio donde se encuentra el archivo-m). Borrar la línea lsim y agragar lo siguiente en el archivo-m y correrlo para ver la respuesta con el agregado de la precompensación Nbar.

     Cn=[1 0 0 0];
     Nbar=rscale(A,B,Cn,0,K)
     Bcn=[Nbar*B];
     [Y,X]=lsim(Ac,Bcn,Cc,Dc,U,T);
     plot(T,Y)
     legend('Carro','Péndulo')

Tuvimos que usar una matriz C distinta porque rscale no está preparada para más de una entrada. Sin embargo, la Nbar calculada es correcta, como puede verse de la salida:

   Nbar = -70.7107

Ahora el error estático está dentro de los límites deseados, y los demás requerimientos de diseño se satisfacen.

Diseño del Observador

La respuesta es buena, pero asume la disponibilidad de todas las variables de estado para la realimentación, que no suele ser el caso en general. Para solucionar esto, diseñamos un observador de orden completo y estimamos aquellos estados que no se miden. El esquema del sistema con observador es el siguiente, sin Nbar:

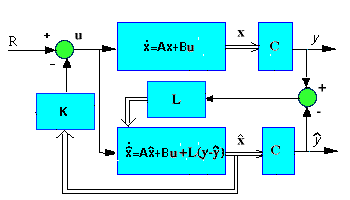
Para empezar, tenemos que encontrar los polos del sistema controlado. Para hacer esto copiar las siguientes líneas de código al final del archivo-m:

   p = eig(Ac)

Si los pesos x e y fueron cambiados a x=5000 e y=100, deberían obtenerse los siguientes polos en la ventana comando de Matlab:

   p =
      -8.4910 + 7.9283i -8.4910 -7.9283i -4.7592 + 0.8309i -4.7592 - 0.8309i

Queremos diseñar un estimador que sea unas 4 a 10 veces más rápido que el polo más lento, digamos en -40. Usamos la función place en Matlab para encontrar el vector L (noter que acker también puede usarse, o los métodos de la ecuación de sylvester de Chen). Recordar que la función place no puede tener todos los polos en la misma posición para una sola entrada de control. Borrar desde el comando lsim en adelante y agregar las siguientes líneas al final del archivo-m para encontrar la matriz L:

     P = [-40 -41 -42 -43];
     L = place(A',C',P)'

Usamos las dos salidas para diseñar el observador (ángulo del péndulo y posición del carro). El sistema no es observable si sólo se usa el ángulo del péndulo como salida; lo que puede comprobarse calculando la correspondiente matriz de controlabilidad y calculando su rango (rank(obsv(A,C(2,:)))). Esto es lógico, ya que si sólo sabemos el ángulo del péndulo no hay forma de inferir la posición del carro de esta información.

Debería obtenerse lo siguiente en la ventana de comando de Matlab:

     L = 1.0e+03 * 0.0826 -0.0010 1.6992 -0.0402 -0.0014 0.0832 -0.0762 1.7604

Ahora combinamos el controlador con el observador para construir el compensador completo. La respuesta debería ser similar a la que obtuvimos cuando diseñamos la realimentación de estados. Para armar el compensador copiar lo siguiente al final del archivo-m:

     Ace = [A-B*K B*K; zeros(size(A))
     (A-L*C)];
     Bce = [ B*Nbar; zeros(size(B))];
     Cce = [Cc zeros(size(Cc))];
     Dce = [0;0];
     T = 0:0.01:5;
     U = 0.2*ones(size(T));
     [Y,X] =  lsim(Ace,Bce,Cce,Dce,U,T);
     plot(T,Y) 
     legend('Carro','Péndulo')

Después de correr el archivo, deberíamos obtener la siguiente respuesta al escalón del sistema:

La respuesta es adecuada con un mínimo de esfuerzo de control, por lo que concluimos el diseño acá sin más iteraciones.

Como vemos, es bastante fácil diseñar controladores para sistemas MIMO via espacio de estados.